
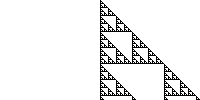


 |
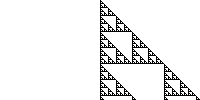 |
 |
 |
A cellular automaton is a simple parallel machine. Its current state is defined by a field of cells. These cells can be in a number of states, as indicated by their colour. Every time-step, the cells in the simulation change their state simultaneously. They regard their own state, and the state of their neighbours to determine their new state.
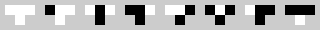 |
| Rule 110 |
|---|
The preceding figure defines an automaton. Each cell looks at a 3 cell wide context to compute its successor state. For example, when a cell is white and its two neighbours are black, it becomes black in the next step. (As shown by the third pattern from the right) All cells change their state at exactly the same time.
The next figure demonstrates the rule shown above. The first row gives the configuration of the cell field at a given time-step. Each cell applies the rules as given above, in parallel. This yields the second row. The cells at the border of the field consider their neighbours white. The title figures show four different automata applied at a field containing initially just one black cell. The figure below is an excerpt from the right-bottom title figure.
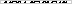 |
| Step 150 and 151, using rule 110 |
|---|
Note that in the introduction we use only two colours, and a three cell context, for reasons of simplicity. In general, cellular automata can use any number of states and context lengths. They even can be higher-dimensional, as in John Conway's 2D Game of Life.
Cellular automata are very simple machines that can expose highly complex behaviour. There exist Turing Complete and Universal cellular automata. This means that cellular automata are (among others) in fact the most powerful machines we currently know to exist.
On the other hand, the majority of cellular automata are not interesting. They generate constant or simple periodic images.
This product automates the search for the interesting cellular automata. It approximates the complexity of the generated pattern using off-the-shelf compression technology. It subsequently uses a simple generate and test approach to find interesting cellular automata.
The program proposes the following parameters:
states | Number of states in the simulation |
context | Context extent of the rules. The context length is given by 2*context+1 |
initial | Number of randomly generated initial cells |
generations | Number of generations to simulate |
complexity | Minimum complexity to search for |
The program executes in three stages:
states and context context lengthinitial, and apply the rules generations steps.
The program repeats these three steps until it finds a resulting complexity higher than complexity.
There are states states. A context is per definition a list of 2*context+1 states. To specify an automaton, one needs to give the successor state for every possible context. This leads to the following formulae and numbers:
| Number of contexts | states(2*context+1) |
|---|---|
| Size of an automaton | log2(states)*states(2*context+1) bits |
| Number of automata | statesstates(2*context+1) |
states | context | size of automaton | number of automata | ||||
|---|---|---|---|---|---|---|---|
| 2 | 1 | 23 | = | 8 | 223 | = | 256 |
| 2 | 2 | 25 | = | 32 | 225 | = | 4.3 109 |
| 3 | 1 | log2(3) 33 | = | 43 | 333 | = | 7.6 1012 |
| 2 | 3 | 27 | = | 128 | 227 | = | 3.4 1038 |
| 3 | 2 | log2(3) 35 | = | 386 | 335 | = | 8.7 10115 |
The case states=2, context=1 has been studied in depth by Stephen Wolfram. He found that in this case the automata with Wolfram Number
30 GIF (155 KB), 60 GIF (25 KB), 90 GIF (30 KB) and 110 GIF (46 KB) were particularly interesting. These automata (and their symmetric counterparts) and a couple of other interesting automata are easily found with complexity=10000. The automata given by these numbers serve as the title pictures of this page.
In every other case, the combinatorial explosion prevents us from systematically enumerating and testing all automata. Luckily, the size of a single automaton remains small. We can therefore simply generate automata, and test them. My program does exactly this, and their results are promising: See for example: automaton 4462648359618 GIF (418 KB)
Cellular WorkmateThe program is written in Java. For building it uses ant (an open-source, platform independent, xml-based, dependency tracking, fast build tool for java projects from the Apache community).
The program is copyright 2004 by Wouter Koolen-Wijkstra. It is released under the GNU GPL
| executable | jar (35 KB) |
|---|---|
| full source | gzipped tar archive (18 KB) |
The program needs a Java Runtime Environment (For example Sun's J2SE JRE) to execute. Execution with java -jar Cellular.jar or double-click under Windows.
Java comes with a built in gzip compressor, which is used by the program. Furthermore, the program interfaces with the external programs gzip, bzip2 and PPMd when they are available. The modular structure of the program makes it very easy to add other (java or external) compressors.
Currently the program runs all compressors to completion, even when a compressor already outputted a size below the demanded minimum complexity. This is really unnecessary, but it is difficult to do proper cleanup when the executing compressors are killed.